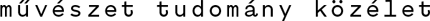Vegyünk egy ilyen burkolásra alkalmas geometriai (alap)alakzatot – például négyzetet. A szomszédait ebből két különböző irányú eltolással kapjuk, ezek szomszédait rendre úgy, hogy az előző eltolásokat ezekre is alkalmazzuk, „és így tovább, ezt az eljárást folytatva a végtelenségig”. Ha ezzel készen vagyunk, vagyis az alapalakzattal burkoljuk a síkot, akkor ennek egy újabb eltolásával ugyanazt a kikövezett síkot kapjuk. Nos, az ilyen kövezést nevezzük periodikus kövezésnek, csempézésnek vagy parkettázásnak. Amit ebből a gondolatmenetből nyomon követhetünk, az többnyire a konstrukció rajza, a kikövezett sík egy véges darabja.
Több ezer éve ismert, hogy szabályos háromszöggel, négyzettel vagy hatszöggel periodikusan kikövezhető a sík. Ráadásul úgy, hogy minden kő élben legfeljebb egy másikkal, csúcsban pontosan ugyanannyival szomszédos. Ha a kövek mindegyikére más-más valamit rajzolunk rá – jobb ötlet híján megszámozzuk őket –, és azt mondjuk, hogy két kő csak akkor azonos, ha a mintája is azonos, akkor máris megkaptuk a sík nem periodikus, azaz aperiodikus kövezését. Ez esetben nem létezik olyan eltolás, amely a kikövezett síkot önmagába viszi.
Maradjunk még a periodikus kövezésnél. Ha egyféle kövünk van – mondjuk, téglalap alakú –, akkor ezzel már igen változatos mintákat tudunk kirakni. A változatosság gyönyörködtet, mondjuk, a mintakészítés pedig már művészet. A művész kitalálja, a műélvező gyönyörködik benne. Nem kell hozzá sok dolog. Elég például kiköveznünk a síkot négyzettel, ezzel egyenértékű módon téglalappal vagy paralelogrammával. Ha ennek a – például – téglalapnak a szemközti éleit találomra valahogyan cikcakkosra deformáljuk, a szemköztit ugyanígy (megtartva azt a tulajdonságot, hogy a szemközti határvonalak egy eltolással egymásba vihetők legyenek), máris figyelemreméltó egyedi követ vagy csempét kaptunk a téglalapból. Kitűnő példa erre Maurits Cornelis Escher Szabályos térfelosztású lovak című közismert műve. A recept egyszerű. Vegyünk egy téglalapot; osszuk ketté a középvonala mentén; egyik felére rajzoljuk ilyen vonalakat, ezt a rajzot tükrözzük a téglalap másik középvonalára, majd toljuk el az eredeti téglalap másik felére. E vonalak mentén daraboljuk fel a téglalapot, majd az így kapott részeket illesszük össze a szomszédjaikkal. Ezzel előállítottuk a kövezés alapelemét, amely ez esetben egy sötét és egy világos lovas. Egyszerű. Nem? Hát… Nem! Ettől művészet a művészet.

Maurits Cornelis Escher: Szabályos térfelosztású lovak
Bizonyítható, hogy a síkban az egybevágósági transzformációknak összesen tizenhét különböző csoportja – alapmintája – van, amelyek alkalmazásával a sík periodikusan lefedhető. Escher mindegyiket ismerte és alkalmazta.
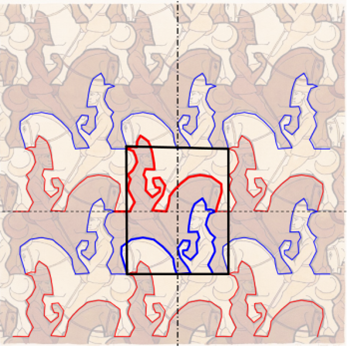
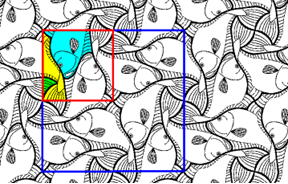
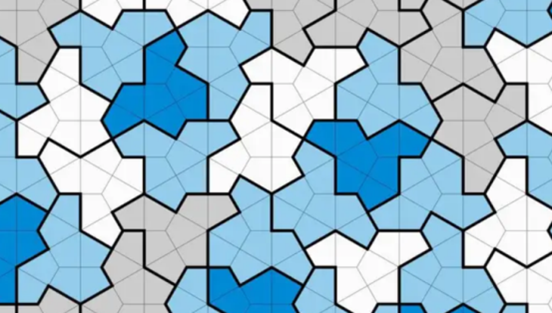
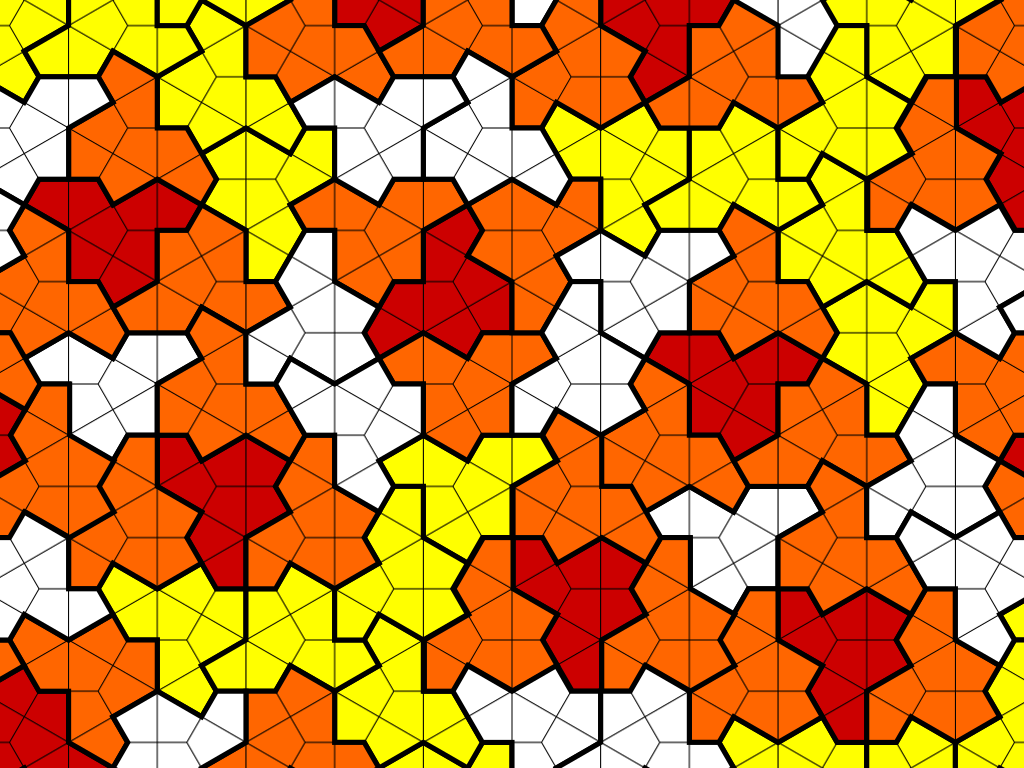
Vegyünk ezek közül még egyet, amely kairói csempe névvel került be a matematikai köztudatba. A nevét a Kairóban lefényképezett, kétes tisztaságú járdáról kapta. „Gyönyörű!” – kiáltott fel elragadtatással az ilyesmivel (is) foglalkozó matematikus, amikor a képet meglátta. Többünknek alighanem a jobb oldali rajz nyeri meg inkább a tetszését. Rajta tisztábban szemlélhető a geometria sokszínűsége. Bár a színek megválasztása azt sugallja, hogy az ötszögek kiemelkedhetnek a síkból, de igazolható, hogy ez nem így van. Itt az eltolásokat vezérlő klaszter négy, különböző színű ötszögből álló, úgynevezett affin szabályos hatszög, amelynek a szemközti oldalai párhuzamosak és egyenlők.

Itt is egyszerű a recept: vegyünk egy tetszés szerinti háromszöget, két oldalára illesszünk az átfogójával egy-egy egyenlő szárú derékszögű háromszöget. Ezzel kapunk egy általános kairói csempét, amelynek az affin szabályos hatszög klasztere négy egybevágó ötszögből áll.


Roger Penrose a róla elnevezett csempék előtt

"Az Ön rendszerében két alakzattal, a »dárdával« és a »sárkánnyal« készül a sík nem periodikus lefedése. Elképzelhető, hogy létezik egyetlen alakzat is, amellyel nem periodikusan csempézhető a sík?
Abban a cikkben, amelyik legközelebb jutott ehhez a kérdéshez, a válasz attól függ, milyen szabályokat fogadunk el az illeszkedésre. Bizonyos szempontból a szabályok egy-egy extra csempével helyettesíthetők. Amennyiben egymásba illő csempéket követelünk meg, akkor legalább három ilyenre van szükségünk, de kettőre levihetjük a számukat."
Penrose aperiodikus csempéinek igen komoly irodalma és tudományos hatása van: az úgynevezett ötödrendű szimmetriát alkalmazó kvázi kristályok elmélete és főként gyakorlati alkalmazásai. Ugyanis ezt megismerve a kristálytan szakemberei először azt mondták, mint aki először látott zsiráfot: ilyen állat nincs. De mégis van! Sőt, mint látjuk, nemcsak a tudományban.
Ezzel együtt az aperiodikus csempék témakörében 1974 óta semmilyen igazán új eredmény nem született. Mígnem 2022-ben David Smith nyugalmazott angol nyomdatechnikus és műkedvelő matematikus egy puzzle-készlet előállítására alkalmas szoftverrel felfedezett egy sokszöget, amelyet kalapnak nevezett, és amelynek egybevágó példányaival aperiodikusan kikövezhető a sík, sőt ez az alakzat nem is alkalmas periodikus kövezésre egyáltalán. Erről ő és három diszkrét geométer, Joseph S. Myers, Craig S. Kaplan és Chaim Goodman-Strauss idén márciusban közzétett egy elemzésre, bírálatra szánt dolgozatot. A diszkrét jelző nem arra utal, hogy a szerzők tudnak titkot tartani – nem is szeretnének –, hanem arra, hogy diszkrét geometriával foglalkoznak, azaz metrikus és kombinatorikus szempontból vizsgálják a geometriai objektumok tulajdonságait.
A cikk alapján úgy tűnik, hogy a kalapokból összeállítható néhány klaszter hézagmentesen kitölti a sík egy részét. Ezek a síkrészek egymáshoz is illeszthetők úgy, hogy egy-egy nagyobb klasztert alkotva ismét síkkitöltők legyenek, és mondható: „és így tovább”. Bár, ez az „és így tovább” talán még nem eléggé meggyőző. De hát mindannyiunk számára adott a kételkedés joga – és kötelessége.
David Smith kalapjának a csúcsai láthatóan egy szabályos hatszögrácsot, illetve annak csúcspontjait képezik. Vegyük észre, hogy a sötétkékek ellentétes körüljárásúak a többivel. Így bár valóban egyetlen alakzat elegendőnek tűnik az egész sík lefedéséhez, ehhez a „jobbos” és a „balos” változatok egyaránt kellenek. A szerzők szerint az egyikből durván négyszer annyi kell, mint a másikból. Ráadásul az igazi követ nem tehetjük le a visszájáról. Ezért ezt a kövezést gyenge egyelemű aperiodikus kövezésnek nevezték a szerzők. Az alakzatot pedig „Ein Stein”-nek (’egyköves’-nek) nyilvánították. A szójátékon még az is felkapja a fejét, akit különösebben nem hoz lázba az egyelemű aperiodikus csempézés problematikája.
A tanulmány szerzői azt is megmutatták, hogy ennek a síkkitöltő alakzatnak a formája – bizonyos határok között – változtatható. Így találták meg azt a változatot, ahol a kövezéshez nem kell – sőt nem is lehet – váltogatni a jobbos és balos elemek között, a lefedéshez minden elemnek azonos kiralitásúnak (körüljárási irányúnak) kell lennie. Ez már erős egyelemű aperiodikus kövezés.
Mindezt májusban újabb dolgozatban írták le, ahol – szellemes módon – szellemnek, kísértetnek (spectre) nevezték az alapelemet.
A „szellem” elveszítette azt a tulajdonságát, hogy a csúcsainak a koordinátái könnyedén megadhatók. Ez maradjon az ezzel foglalkozó matematikusok gondja. Viszont észrevehetjük, hogy az oldalai egy kivételével egységnyiek, az két egységnyi. A szögei felváltva kilencven és százhúsz fokosak, bár akad két kilencven és százhúsz fokos is, amelyik ellenkező irányú, mint a többi. Ez a leírás persze kevés ahhoz, hogy ez alapján egyértelműen megadjuk – elképzeljük – az alakzatot. Látni kell!


Ki tudunk tehát alakítani kilenc „szellemből” egy klasztert, kilenc klaszterből egy nagyobbat. Ez persze így még csak játék a formákkal. Az igazi kérdés matematikai szempontból továbbra is az, hogyan építhetők egyre nagyobb és nagyobb egymáshoz illeszthető klaszterek, amelyek biztosítják a sík egyrétegű, hézagmentes lefedését. Vagyis működik-e az „és így tovább” szigorú elve: vajon valóban kikövezhető a sík ilyen „szellemekkel”?
A legtöbbünket ennél egyszerűbb kérdés foglalkoztat. Vajon lesz-e valaha ennek az önmagában is szép matematikai konstrukciónak gyakorlati haszna, vagy találkozhatunk-e vele például egy figyelemreméltó képzőművészeti alkotásban?
Addig is a homo ludens érdeklődésével felruházott, szellemi kalandokra fogékony emberekként bizonyára szívesen vennénk kezünkbe ezeket a „szellemeket” nem az egész síknak, hanem csak egy kis darabjának a lefedése céljával. Ugyanis még az sem biztos, hogy csak az az egyetlen járható út, amelyet az említett cikkek szerzői mutattak be.
A szerző matematikus, az egykori szegedi tanárképző főiskola oktatója, a Szilassi-poliéder alkotója, részletesebb írása a témáról itt olvasható
Nyitókép: Orosz István: Könyvtár III. (részlet)